Rotational Motion Problem Set

Rotational Motion		Home Problem Sets Kinematics Momentum Rotational Motion Energy Background Theory Goals Current Voices Note on Stereotypes Guidelines References Project History Timeline Authors Acknowledgements Project Evaluation Links Download Problems

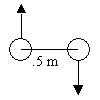
	1) Physics on Ice Canadian figure skaters Jamie Sale and David Pelletier, gold medalists in the 2002 Olympics, are practicing a new move. Jamie, whose mass is about 50 kg, skates towards David at 4.5 m/s. David’s mass is 56 kg and his speed is 4 m/s towards her. They grab hands as they pass each other, with their center of masses about .5 m apart, and briefly go into a tight spin. Then they both extend their arms so that they are about 1.4 m apart and spin more slowly. What is conserved in the “collision” when they grab hands: linear momentum, angular momentum, total energy, kinetic energy? Why or why not? What is their total kinetic energy before they grab hands? What is their total linear momentum before they grab hands? What is their total angular momentum before they grab hands? After they grab hands, what is their moment of inertia, if we approximate them as two point masses? What is their angular velocity? What is their rotational kinetic energy? What is their moment of inertia when they extend their arms? What is their angular velocity then? What is their rotational kinetic energy then? Why is their energy different now? What happened to it? 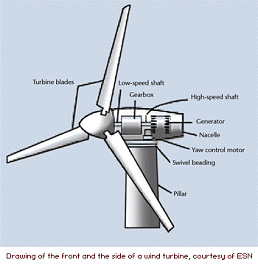2) Making a Wind Turbine www.bergey.com You are designing a wind turbine for a small ecovillage. You have constructed a turbine with a 197 ft. tower and a 151 ft rotor diameter. The generator you are planning to use requires 1200 rpm, but with current wind speeds, the rotor shaft spins at only 24 rpm. If the rotor shaft was connected directly to the generator, how fast would the tips of the blades spin when the necessary speed was reached? Is this feasible? What might you construct between the rotor shaft and the generator to mitigate this problem? 3) Canned Veggie Races Ravi and Kamal are playing, rolling items down a wooden board set at an angle. Ravi has a full can of vegetables and Kamal has an empty one, and they are going to see whose can gets to the bottom of the incline first. Kamal, who has studied some physics, believes that they will both reach the ground at the same time because the acceleration of gravity is constant. The full can has a mass of 468 g, the empty one has a mass of 56.7 g, and both have a radius of 4 cm. The 1 m long board is propped up so that one end is about .2 m above the ground. Whose can gets to the bottom first? How long does it take Kamal’s can to roll down? How long does it take Ravi’s can? After the first race, Ravi runs inside and grabs an empty coffee can, whose mass is about the same as the empty tin can but with a radius of 8 cm. How long does it take this can to roll down the incline? Top 4) Physics of Wind Turbines www.bergey.com A small wind turbine designed for household use has three blades made of high-density fiberglass ( r = 90 kg/m 3). The blades are 2.5 m long, and approximately 14 cm square in cross section. What is the moment of inertial of the turbine? If the turbine is spinning at 25 rpm, what is its angular momentum? If the wind gets too strong, it can be necessary to such down the turbine to prevent damage. If the turbine is spinning as above, how much torque must be applied to stop the turbine in 60 s? 5) Gearbox In a wind turbine, a gearbox connects the low-speed shaft (the one connected to the rotor) to the high-speed shaft (the one connected to the generator). Typically, the gearbox has a ratio of 50:1, and rotates at 1200 rpm. The turbine has a rotor diameter of 144 ft. a) What is the angular velocity of the high-speed shaft? b) At what angular velocity will the low-speed shaft spin? How fast will the tips of the blades be moving? c) Most generators have an upper limit on their rotational speed, to prevent damage. If your generator’s limit is 1500 rpm, what is the maximum velocity of the tips of your rotor blades? 6) Somersaults a) Your 4 year-old little cousin, Carmen, is learning how to do a somersault by starting on a 15 ° inclined mat. Assuming your 16 kg cousin scrunches herself into a disk with radius 17 cm, how fast will she be rolling after one 1 somersault (1 rotation?) b) What is the angular speed and the speed at the top of Carmen during her roll? c) After several tries, Carmen has mastered the somersault on the incline mat. She wants to try it on the floor but is having trouble getting started. Being the nice cousin that you are, you push her the first 1/8 of her roll. How much force do you have to apply to get her to continue rolling at the same velocity and angular momentum as above? (Hint: use what you know about work, K.E. and torque.) 7) Diving World Cup At the 1999 FINA Diving World Cup 3m competition, 22 divers did a back 2 ½ somersault in a tuck position. The remaining 6 did their back 2 ½ in the pike position. On average, those that chose to do the dive tuck left the board at an angle of 70 degrees, and were in the air for 1.3 seconds. Jenny Keim from the United States did her back 2 ½ in the pike position. If she was also in the air for 1.3 seconds but left the board at angle of 64 degrees. Wu Minxia from China was in the tuck position. a) Why do Jenny and WU have to leave the board at different angles? b) The tuck divers spend about 0.65 seconds in the tuck position. If WU spends about 2 rotations in the tuck position, what is her tuck angular speed? The rest of the dive is in the straight position, what is this angular speed? c) What is the ratio of moments of inertia? d) WU Minxia is 164 cm and weighs 50 kg. Assuming divers gain all their angular momentum from the board, what’s the average torque applied to WU in the 0.2 seconds that the board pushes up on her feet? (Hint: while on the board, the diver is a straight rod rotating around one end.) e) What is the average force on WU from the 3m board for a back 2 ½ somersault tuck? We don’t know if Jenny and WU actually did these dives at the meet. Top Rotation Answers

Posted on 8/1/05 © 2000-2005 Physics For Everyone. All Rights Reserved. Read our Legal Statement and Privacy Policy