|
Home
|
|||||||
5.1) Joe's Job Joe the pony is used to help pull water from a well. His owner wants him to pull up large tubs of water, as much as 80 kg, in each load. Joe is a rather petite pony and can only exert .7 hp of power.
5.2) The Nuclear Alternative A small town consumes about 10 MW of electricity. Currently the town is using a coal-fired power plant to provide this power, but they are concerned about greenhouse gases and global warming, and are wondering whether to close down their plant and begin to buy electricity from a nearby nuclear power plant. Both plants operate at about 34% efficiency. The coal-fired plant uses coal with an energy content of 29.3 J/kg, and every kg of coal (assumed to be pure C, with a molecular wt of 12 g) produces 3.67 kg of CO 2, while the nuclear plant uses uranium enriched to 4% U-235. A gram of U-235 produces 2.56 x 10 10 J.
5.3) Fun in the Sun Solar energy is one of the most important components of a renewable energy future. Your parents are considering installing photovoltaic cells, which convert the sun’s energy directly into electricity, on their roof, and have asked for your help. You do some research and learn that, on a sunny day in Colorado, sunlight at the earth’s surface provides about one kilowatt/m2. Solar panels have an area of 0.5 m2, operate at 10% efficiency, and cost $63. Your parents use electricity at a rate of 2 kW.
5.4) Earthquake The energy of earthquakes comes from the stresses which build up as the tectonic plates on the earth’s surface shift. An earthquake’s strength is typically given on the logarithmic Richter scale. In the past, scientists approximated the energy released by an earthquake from its magnitude, but modern technology allows us to measure the energy released, then determine the earthquake’s magnitude. The old formula for converting Richter magnitude to energy is log E = 4.8 + 1.5Ms , where E is seismic energy in Joules and Ms is seismic magnitude.
5.5) MagLev Trains It takes about 560 kW to run a typical diesel locomotive at speeds around 110 mph. Magnetically levitated, or MagLev, trains, on the other hand, require substantially less power because the magnetic levitation eliminates energy loss to friction. The worst MagLev system requires 270 W to levitate the train and 783 W total to move it at 100 mph (fast MagLevs can make closer to 300 mph). The number of passengers each train can hold is comparable. How much less energy does it take to travel one mile in a MagLev train as opposed to one mile in a train pulled by a diesel locomotive?
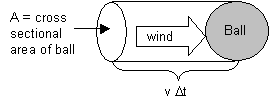
5.6) Kickball It is a beautiful day, so Jamal and his friends are playing kickball at the park. Just as he winds up for his kick, the wind, which is blowing directly toward him, suddenly picks up speed. Despite his strong kick, the ball lands barely 10 feet in front of him. What happened? Can you derive an equation to describe the kinetic power of the wind, and explain to Jamal why his kick was not successful? [Hint: Derive an equation for the kinetic energy the wind is delivering to the ball in one second. Consider the kinetic energy in the volume of air that will impact the ball in one second.
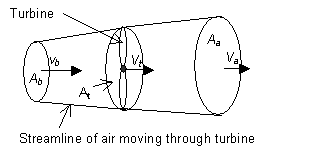
5.7) Catching the Wind Wind turbines are one of the most promising sources of renewable energy today. The problem above shows that the kinetic power of the wind is:
where ris the density of the air, A is the area swept out by the turbine blades, and v is the speed of the wind. Doing some research on wind turbines, you find out the a practical turbine can convert about 40% of that power into electricity. That doesn’t sound like a lot, but is it? If the average household requires 3 kW of power, and the average wind speed is 14 mph, how big a rotor would a household require? (Assume the density of the air is 1.3 kg/m3.) 5.8) Wind Farm On the bus ride home from school, Ignacio and Mariella pass a wind farm. As they are both taking physics, this is naturally of interest to them. Ignacio says that wind turbines can only convert about 30% of the wind’s power, but Mariella is positive that an efficient turbine can do better than that. Derive an equation for the maximum power a wind turbine can extract, and settle this argument.
5.9) Earthship Some friends of yours are planning to build an earthship near Lamar, Colorado, and live off the grid. They would like to install a wind turbine to satisfy their electricity needs, and, knowing you are a physics student, have asked you to help them design their system. You look on a wind map and determine that the average wind velocity at 10 m above the ground in Lamar is 5.2 m/s, and that the air density is 1.0 kg/m3. Small, high efficiency windmills can convert 45% of the wind’s power into electricity. Your friends think that they will need 1 kW of power to meet their needs.
5.10) Biking Power A trained bicyclist in excellent shape might be able to convert food energy to mechanical energy at a rate of 0.25 hp for a reasonable length of time. Imagine such a person pedaling a stationary bike connected to a perfectly efficient electrical generator.
5.11) Hydroelectric Generators Suppose a hydroelectric generator running on pumped storage is required to provide its full power of 200 MW for a period of 8 hr.
5.12) Power of the Wind Suppose one has a propeller-type windmill with blades 1 m long. What is the area swept out by the blades? If the overall efficiency of the windmill is 50%, what is the power produced when the wind speed is 1 m/s (about 2.2 mph)? At 2 m/s? At 10 m/s? 5.13) Eliminating CO It might be proposed that we eliminate excess CO |
|||||||
Posted on 8/1/05 © 2000-2005 Physics For Everyone. All Rights Reserved. |
|||||||