|
Home
Project Evaluation
|
|||||||
1.1) Harvesting the field A farmer sets out to harvest a field of wheat using a combine that is 25 ft. wide and has a top speed in the field of 1.8 m/s. Its acceleration can be described by the function a = ½t, until it reaches its top speed, when the acceleration drops rapidly to zero. Find expressions for the acceleration, velocity, and position. At what time does the combine reach its top speed? Draw a graph of the position, velocity, and acceleration versus time, for the first 5 seconds. 1.2) An elephant lunch
An elephant shakes a tree with her trunk in order to get down some of the seed pods for food. If the lowest branches of the tree are 3 m above the ground, how long does it take for the seed pods from these branches to fall to the ground, and how fast are they falling when they do reach the ground? (Assume no air resistance) A baby elephant catches one of the seed pods that fell from the top of the tree (6 m high), grabbing it with her trunk at 1.5 m above the ground and stopping it 0.3 s later at 0.5 m above the ground; what was the seed pod’s average acceleration between the time it was caught and the time it was stopped? 1.3) Equine Acceleration
As a stablehand, it’s your job to set the horses loose, one by one, into the pasture after the morning feed. When you release a particularly spirited chestnut quarter horse, she takes off from a standstill into a gallop, reaching top speed 6 seconds later by the time she passes a tree 15 m away. You think she might be going 25 mph judging from the comparatively familiar speeds of cars. What is her average acceleration between the gate and the tree (in m/s)? 1.4) The Cat Who Loved Cheesecake
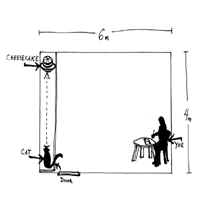
Your dad has just made a cheesecake and has set it on the counter in the corner of the kitchen. He is temporarily occupied, tactfully trying to get a long-winded friend off of the phone; Grymalkin, your most mischievous cat (who also happens to love cheesecake) has just entered the kitchen door and, spying the cheesecake, jumps onto the counter right by the door and begins trotting towards the cheesecake at a constant velocity of 1 m/s. If you are sitting in the opposite corner of the kitchen what does your average acceleration need to be in order to get to the cheesecake before the cat? The dimensions of the kitchen are 4 m by 6 m. (drawing not yet scanned) 1.5) Mountain Mamas You get up at the crack of dawn one morning to go mountain biking with a friend. On a narrow downhill section of the trail, you let her go first, since she’s eager to try out her new clipless pedals. You’re riding along at a constant velocity of 4 m/s when you turn a corner and see that your friend has stopped to watch a deer in the woods; you don’t want to become an entangled mess of arms, legs and bike frames, so you’d like to be able to stop before you reach her position on the trail, a little over 4 meters from you now. If your braking acceleration on the downhill, gravel trail is 3.6 m/s2, can you stop in time before scaring the deer away with your messy entanglement? If your average velocity riding uphill on your mountain bike is about 5 mph, and your average velocity when riding downhill is about 16 mph, and you spend approximately 3 hours going uphill, about how long will it take you to ride down the mountain by the same route that you rode up? 1.6) The Windy City You would like to take the bus from a theater in downtown Chicago back home to your apartment—it’s a windy, freezing cold night and all you want now is some hot cocoa. There are two different routes you could take, and you remember that one day when you did some calculations for fun, you discovered that bus A is rather shabby and can only accelerate at 2 m/s2, whereas bus B can accelerate at 4 m/s2. Likewise bus A’s brakes are slightly worse and can only accelerate the bus at –4 m/s2, whereas bus B’s brakes can accelerate the bus at –5 m/s2. However, the average speed limit on bus A’s route is 6 m/s and the average speed limit on bus B’s route is only 4 m/s due to traffic. If the distance to your apartment on route A is 0.72 miles long and the distance on route B is 0.65 miles, and your apartment is the first stop for both routes, which bus actually gets you home faster to your cup of cocoa? 1.7) Life on the plains On the plains of Africa, the grasses, grazing animals and predators have all coevolved. Grazing animals like gazelles depend on speed and endurance to escape from predators. Big cats like cheetahs depend on their stalking skills to get close, and on rapid acceleration to catch their fleeing prey. A cheetah can accelerate from rest to 20 m/s in just 2 seconds. It is the fastest of all animals, with a top speed of 32 m/s. But it can only maintain that speed for about 300 m. A cheetah is crouching in the grass, 50 m from a herd of gazelles when the animals begin to run. They run at 23 m/s, and can keep that up for long distances. Can the cheetah catch its prey, or will it go hungry tonight? 1.8) Speeding ticket Barbara commutes from Castle Rock to Colorado Springs, every day—about 45 miles straight south on the interstate, where the speed limit is 75 mph. If she drives at 85 mph, how much time does she save on her daily round trip? How does this compare to the 20 minutes she spends talking to the policeman who gives her a speeding ticket? |
|||||||
Posted on 8/1/05 © 2000-2005 Physics For Everyone. All Rights Reserved. |
|||||||