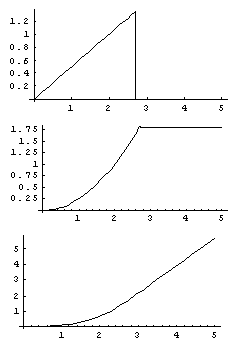
Answer 1.1: Expressions: a = ½ t until top speed is reached, a = 0 after that

v = ¼ t 2 (assuming the combine starts from rest)until top speed is reached, v = 1.8 m/s after that

x = 1/12 t 3 (assuming the initial position is labeled x = 0) until top speed is reached. After that it increases linearly.

The combine reaches its top speed at t = 2.7 s

Graphs 1,2,3

1 is v vs t(s), 2 is x vs t(s) and parabolic, 3 is cubic, linear

a (m/s 2)

t (s)

Answer 1.2: The seed pod hits the ground 0.78 s after it leaves the branch, at a velocity of 7.6 m/s.

The average acceleration of the seed pod the baby elephant catches is 3.1 m/s 2, directed upwards.

Answer 1.3: 1.9 m/s 2

Answer 1.4: It will take Grymalkin 4 s to get to the cheesecake. In order to get diagonally across the kitchen (7.2 m) in 4 s, you need to accelerate from rest at an average of 0.9 m/s 2

Answer 1.5: You will stop in about 2.2 meters from your present position on the trail, or 1.8 m in front of your friend.

It will take you 56 minutes to ride down.

Answer 1.6: Bus A takes 3 minutes and 17 seconds to get there; Bus B takes 4 minutes and 26 seconds; therefore Bus A is faster.

Answer 1.7: After 300 m, the cat is still behind the gazelle.

Answer 1.8: At the speed limit, the trip would take her 36 minutes; at 85 mph it will take 32 min. It’s not worth the risk for a four minute gain.

Top

Answer 2.1: t = 0.48 s

Answer 2.2:

Answer 2.3: The ball hits the ground 7.9 m from you. Taku needs to run at 4.5 m/s (10 mph) in order to catch it.

Answer 2.4:

Answer 2.5: a) y-y o = v osinθt – ½gt 2
-3m = v o sin70(1.3s) – ½ (9.8 m/s)(1.3s) 2
v o = 4.3 m/s

b) v o = 4.5 m/s

c) Tuck
x – x o = v ocosθt
= (4.3 m/s)(cos70)(1.3s)
= 1.9m
Pike
x – x o = v ocosθt
= (4.5 m/s)(cos64)(1.3s)
= 2.6m

d) Change in v y = v osinθt – gt
0 = (4.3m)(sin70) –(9.8m/s)t
t = .41s
0 = (4.5m)(sin64) –(9.8m/s)t
t = .41s
y t = v osinθt – ½gt 2
= (4.3m)sin70(.41) -1/2 (9.8m/s)(.41) 2
= 0.83m above the board
0.83 + 3m = 3.83 m above the water
y p = (4.5m)sin64(.41) -1/2 (9.8m/s)(.41) 2
= 0.83m
= 3.83 m above the water

e) v y +v x at t=1.3
v f = (v osinθt – gt) 2 + (v ocosθ) 2
v ft = 7.6 m/s
v fp = 7.5 m/s

Top

Answer 3.1: She should take a direction 36 degrees west of south (216 o by the compass) and travel 0.36 km; it will take her 3 minutes and 59 seconds to get from the first to the second source.

Answer 3.2: The birds should fly at a heading 24 o west of south, or 204 o by the compass. Their speed south is 16 kts, or 18 mph. It will take them 6.4 days to reach Mexico.

Answer 3.3: The wind is contributing 31.9 km/h to her eastward velocity, and subtracting 2.8 km/h from her northward velocity. She is flying at a heading of 45 o with an airspeed of 18.4 km/h.

Answer 3.4: Your initial compass heading should be 272 o, or just a bit north of west. Your speed relative to the ground will be 106 kts.

Answers 3.5:

a) Day 2, just over 5.5 miles

b) Day 5, 3280 ft

c) 18.5 miles (97,601 ft)

d) 2.64 miles/day (13,943 ft/day)

e) 1975 ft/day

Top

Answer 4.1: Dropping bucket: Acceleration vs. Time is a line at 9.8 m/s2 with slope of 0.

Velocity vs. Time is linear with a slope 9.8 m/s2 and with intercept 0.

Position vs. Time is parabolic with final value at 10 m.

Raising bucket:

a (m/s 2)

t (s)

Acceleration vs. Time has an acceleration of 0.1 m/s2 from t=0 to t=5s. Then a=0 until 10.5s where it becomes –1.25 m/s2 until 44.5s where it drops to 0.

Velocity vs. Time: The velocity is 0 at t=0 and then increases to 0.5m/s at 5s. It remains at this value until t=40.5s when it starts decreases to 0 at t=44.5s.

v (m/s

t (s)

Position vs. Time: position parabolically increases concave up from t=0 to t=5 (1.25m) and then linear increases until d=19m (t=40.5). At this point the function is becomes concave down parabolic and finishes at 20m (t=44.5s).

y (m)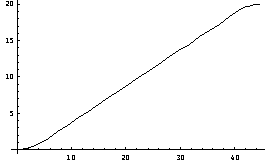

t (s)

Answer 4.2: She has to run 50 minutes

Answer 4.3: The northern path is 1.03 km long while the southern path is 1.62 km long. The trip home carrying water takes 48 minutes on the northern path and 42 minutes on the southern path. So Tsitsi’s preferred route is to walk to the well on the rougher northern path and to come home along the well-beaten southern route. This trip will take her 78 minutes including the 15 minutes at the well.

Answer 4.4: 15 minutes, 6 seconds for red and 7 minutes, 42 seconds for green.

Top

Answer 5.1:

Answer 5.2: The car is initially going straight, along with your sunglasses. When the car turns to the right, it does so because of the frictional force from the road pushing it to the right (we call this centripetal force). Your glasses want to continue in a straight line because of inertia. Because the frictional force holding them to the dashboard is small, they will continue to go straight, sliding to the left relative to the car.4.2: She has to run 50 minutes.

Top

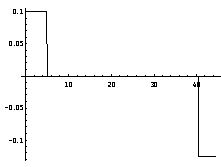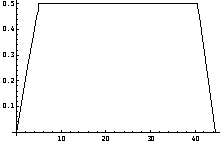Kinematic Problem Sets